Taalit wrote:Yeah, I saw a video on khanacademy about this exact problem and it helped. I need to work on my geometry, I've been skipping out on that stuff. All I know is integrals and whatnot
Well, actually, all geometric formulas can be derived from integrals. (Although perimeter and circumference ones tend to be a bit tricky, especially since the circumference of a circle is usually derived in polar coordinates with radians, which is based on the circumference of a unit circle...>_>)
For example, in the triangle example, the area is merely the double integral of 1, with either the upper y limit or the upper x limit containing the equation for the hypotenuse.
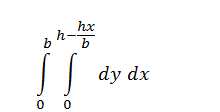
This applies to all triangles, although any non-right triangle will have a continuous piecewise hypotenuse, and thus will require
you to split it into the sum of two separate triangles, which will give you the same formula in the end regardless.
So yeah, once you know integrals...(and polar, cylindrical, and spherical coordinate systems)...you don't need to know geometry anymore, as you have the tools to rigorously prove geometry.
Taalit wrote:Speaking of integrals, I successfully solved this in school today:

It has quite an interesting value!
Wait, are you using log to express the base 10 logarithm, or the natural logarithm?
Either one, that still is quite impressive. That is one I would have resorted to numerical approximations to derive...congratulations!